scipyのポアソン分布を計算するpoisson.pmfの使い方について
今回はscipyのポアソン分布を計算するpoisson.pmfの使い方についてご紹介いたします。
scipyのポアソン分布を計算するpoisson.pmfの使い方について
ポアソン分布は一般的に次の式で表せます。
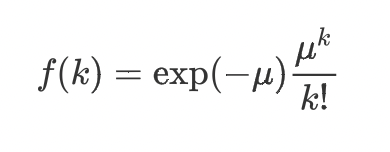
上記のexpはネイピア数のe、μは期待値(λと表される場合も多いです)、kは求めたい発生する確率(所与の時間中に平均でμ回発生する事象がちょうどk回発生する確率)となります。
例えば、「単位時間あたりに10回発生する事象がちょうど2回発生する確率」を求めたいとします。
すると、scipyのpoisson.pmfを使って次のように表すことが可能です。
|
1 2 3 |
>>> from scipy.stats import poisson >>> poisson.pmf(2, 10) 0.0022699964881242435 |
poisson.pmfの一つ目の引数がk(所与の時間中に平均でμ回発生する事象がちょうどk回発生する確率)、二つ目の引数が期待値μとなります。
ちなみに、poisson.pmfは三つ目の引数がありますが、この三つ目の引数はkをずらすのに使います。
例えば、poisson.pmf(2, 10)をpoisson.pmf(2, 10, 1)にした場合は、「単位時間あたりに10回発生する事象がちょうど1回発生する確率」となります。
|
1 2 3 |
>>> from scipy.stats import poisson >>> poisson.pmf(2, 10, 1) 0.0004539992976248486 |
poisson.pmf(2, 10, 1)はpoisson.pmf(1, 10)と同じことで、poisson.pmf(k, mu, loc)はpoisson.pmf(k – loc, mu)と同じ結果になります。
終わりに
今回はscipyのポアソン分布を計算するpoisson.pmfの使い方についてご紹介いたしました。




ディスカッション
コメント一覧
まだ、コメントがありません